Hidden Unit Specialization in Layered Neural Networks: ReLU vs. Sigmoidal Activation
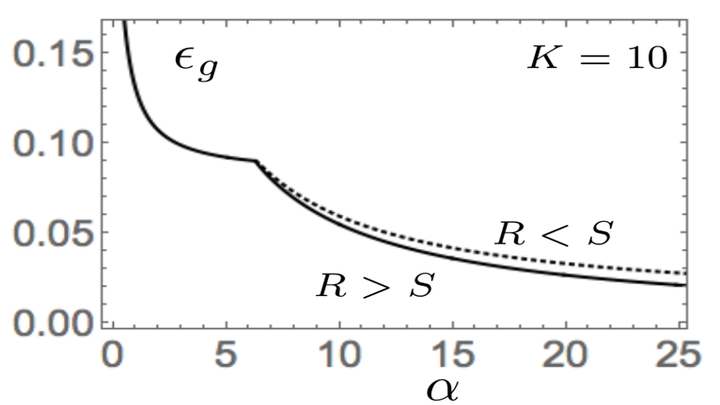Figure: For large ReLU neural networks, phase transitions from unspecialized to specialized hidden unit states are still continuous, as opposed to the discontinuous phase transition observed in sigmoidal neural networks.
Abstract
We study layered neural networks of rectified linear units (ReLU) in a modelling framework for stochastic training processes. The comparison with sigmoidal activation functions is in the center of interest. We compute typical learning curves for shallow networks with K hidden units in matching student teacher scenarios. The systems exhibit sudden changes of the generalization performance via the process of hidden unit specialization at critical sizes of the training set. Surprisingly, our results show that the training behavior of ReLU networks is qualitatively different from that of networks with sigmoidal activations. In networks with K >= 3 sigmoidal hidden units, the transition is discontinuous: Specialized network configurations co-exist and compete with states of poor performance even for very large training sets. On the contrary, the use of ReLU activations results in continuous transitions for all K: For large enough training sets, two competing, differently specialized states display similar generalization abilities, which coincide exactly for large networks in the limit K to infinity.