Statistical Physics of Learning
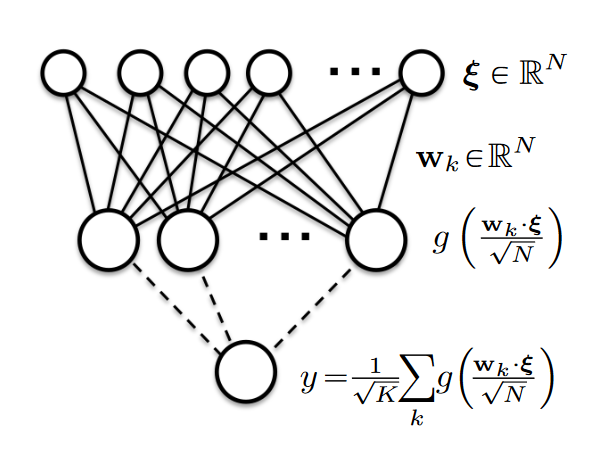 A two-layer neural network with N inputs, K hidden neurons and activation function g(.).
A two-layer neural network with N inputs, K hidden neurons and activation function g(.).
In the deep learning era, many great results are achieved by empirical study. New deep learning methods for typical tasks in for instance computer vision, natural language processing and sound processing are tested on benchmark datasets that are publicly available and have become recognised in the respective fields. This facilitates the comparison of different approaches on these typical tasks. However, in order to make further fundamental progress, the great successes of deep learning in practice should also be supported by more theoretical results.
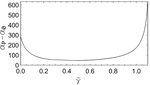
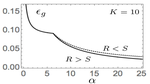
One theoretical approach that has seen renewed interest in recent years is The Statistical Physics of Learning. As the name suggests, it uses statistical physics theory to analyse Machine Learning scenarios. Statistical physics is concerned with modelling the overall properties (macroscopics) of systems that consist of many microscopic entities or particles. A neural network is a machine learning system that consists of many weights (microscopics) that connect neurons, and a configuration of weights realises a certain model with specific properties (macrosopics). The hallmark of The Statistical Physics of Learning approaches are average case results of the main descriptive quantities in machine learning scenarios, i.e. typical results of the training error, the generalisation/test error as well as other summarising parameters of the state of the model, known as order parameters.
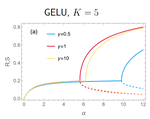
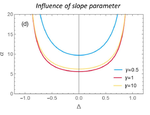
We are using the statistical physics of learning to study recent phenomena in machine learning and also to study potential new approaches for machine learning practice. We are studying typical learning behaviour of models with modern activation functions (ReLU, Leaky ReLU, GeLU) and models in dynamic environments.