Michiel Straat
Postdoctoral Research Group Leader “Lifelong Machine Learning for Physical Systems”
Bielefeld University
Biography
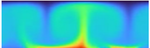
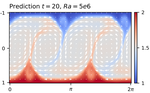
I am a Postdoctoral Researcher and Junior Research Group Leader at Bielefeld University. Our Junior Research Group develops Artificial Intelligence methods for modeling and controlling complex physical systems. Motivated by major global challenges such as climate change and the energy transition, we explore how AI can help understand and model the dynamics of systems in fluid mechanics, and how to enforce desired outcomes through advanced control strategies. A key focus of our research is improving the robustness of these methods under changing conditions and increasing their sample efficiency by using surrogate models and embedding physical knowledge directly into the learning process.
Prior to this, I obtained my PhD (with Highest Distinction) from the University of Groningen, where I was part of the Intelligent Systems group. My doctoral research focused on the theory of neural networks, and I developed a successful predictive maintenance system for a smart factory environment.
Interests
- Machine Learning for Physical Systems
- Fluid Dynamics
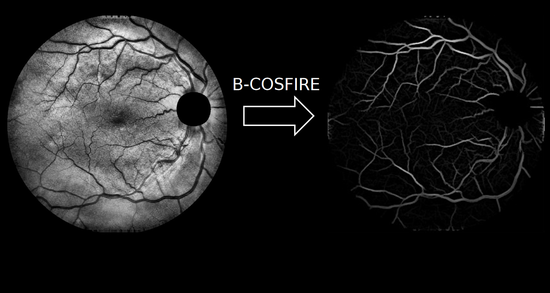
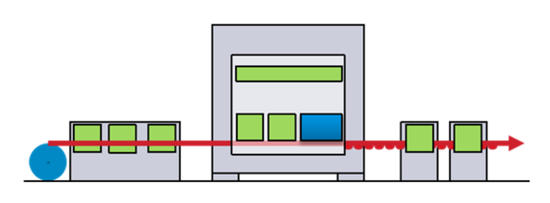
- Industry 4.0
- Theory of Neural Networks
Education
-
Postdoc and Junior Research Group Leader
Machine Learning group, Bielefeld University
-
PhD in Theoretical Machine Learning and Industry 4.0
Intelligent Systems group, University of Groningen, PhD thesis
-
MSc. in Computing Science (specialization: Machine Learning)
University of Groningen