On-line learning in neural networks with ReLU activations
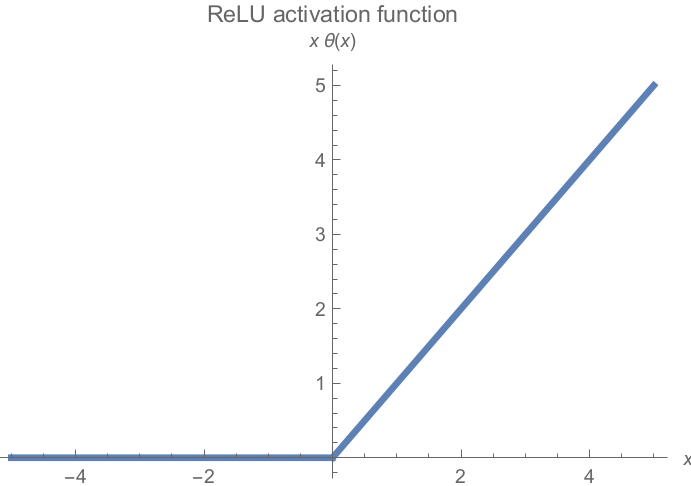 Popular in deep learning: The ReLU activation function.
Popular in deep learning: The ReLU activation function.
Abstract
The rectifier activation function (Rectified Linear Unit: ReLU) has become popular in deep learning applications, mostly because the activation function often yields better performance than sigmoidal activation functions. Although there are known advantages of using ReLU, there is still a lack of mathematical arguments that explain why ReLU networks have the ability to learn faster and show better performance. In this project, the Statistical Physics of Learning framework is used to derive an exact mathematical description of the learning dynamics of the ReLU perceptron and ReLU Soft Committee Machines. The mathematical description consists of a system of ordinary differential equations that describe the evolution of so-called order parameters, which summarize the state of the network relative to the target rule. The correctness of the theoretical results is verified with simulations and several learning scenarios will be discussed.