2025
Solving Turbulent Rayleigh-Bénard Convection using Fourier Neural Operators
I present our publication on the use of Fourier Neural Operator models as surrogates for convection dynamics.

Solving Turbulent Rayleigh-Bénard Convection using Fourier Neural Operators
In this talk I present our work on harnessing zero-shot superresolution surrogate models FNO for convection.
2024
Koopman-Based Surrogate Modelling of Turbulent Rayleigh-Bénard Convection
We presented our work on Koopman-based modeling of Rayleigh-Bénard Convection at the WCCI 2025 in Yokohama.

Koopman-based Modeling of Rayleigh-Bénard Convection
In this talk I will present our recent work on Koopman-based surrogate modeling of Rayleigh-Bénard Convection.
2023
Statistical Physics of Learning
In this talk I discuss the main principles behind the statistical physics of learning.
Modelling adversarial training
In this talk I discuss my recent work on analyzing adversarial training procedures that make machine learning models more robust.
2022
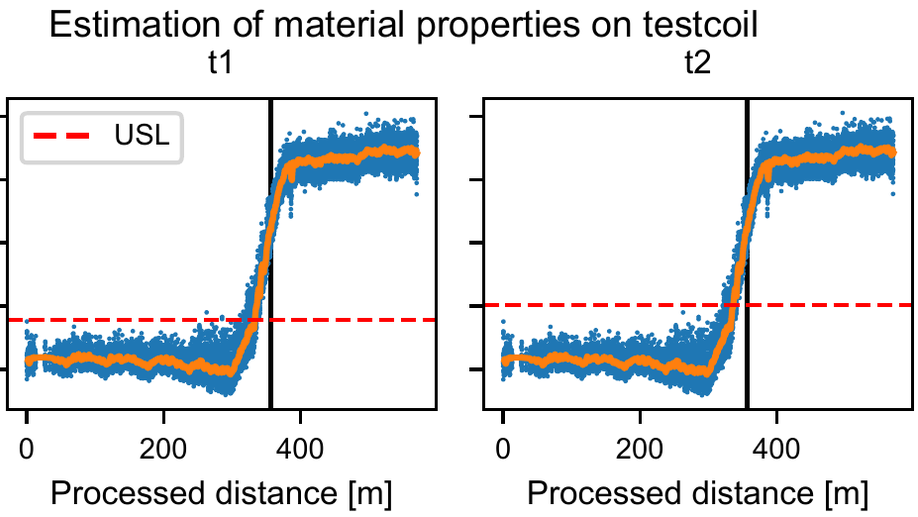
An Industry 4.0 example: real-time quality control for steel-based mass production using Machine Learning on non-invasive sensor data
In this talk a typical Industry 4.0 setting is presented: the use of sensor measurements for real-time quality control and fault prevention.
2021
Feedback Alignment methods for training neural networks
In order to compute weight updates, backpropagation uses complete knowledge of the downstream weights in the network. In [1] it is shown that this can be significantly relaxed by using fixed random weight matrices to transport error signals in the feedback path. The algorithm, termed Feedback Alignment, shows similar performance to backpropagation in several machine learning tasks. In [2] it is shown that even a direct feedback path from the final error to each individual layer results in the learning of useful features and competitive performance compared to backpropagation. In this talk I will briefly introduce the method, give an explanation of how learning arises and discuss results of experiments. I am inspired by
[1] T. P. Lillicrap, D. Cownden, D.B. Tweed, C. J. Akerman, Random feedback weights support learning in deep neural networks
[2] A. Nøkland, Direct Feedback Alignment Provides Learning in Deep Neural Networks
2020
Dynamics of on-line learning in two-layer neural networks in the presence of concept drift
In this talk I will discuss our recent work on learning in non-stationary situations. A modelling scenario of neural networks learning under a random drift process is presented and results will be discussed. Particularly we will focus on the effects of weight decay as a forgetting mechanism.
2019
Online Learning Dynamics of ReLU Neural Networks
The rectifier activation function (Rectified Linear Unit: ReLU) has become popular in deep learning applications, mostly because the activation function often yields better performance than sigmoidal activation functions. Although there are known advantages of using ReLU, there is still a lack of mathematical arguments that explain why ReLU networks have the ability to learn faster and show better performance. In this project, the Statistical Physics of Learning framework is used to derive an exact mathematical description of the learning dynamics of the ReLU perceptron and ReLU Soft Committee Machines. The mathematical description consists of a system of ordinary differential equations that describe the evolution of so-called order parameters, which summarize the state of the network relative to the target rule. The correctness of the theoretical results is verified with simulations and several learning scenarios will be discussed.
2018
On-line learning in neural networks with ReLU activations
The rectifier activation function (Rectified Linear Unit: ReLU) has become popular in deep learning applications, mostly because the activation function often yields better performance than sigmoidal activation functions. Although there are known advantages of using ReLU, there is still a lack of mathematical arguments that explain why ReLU networks have the ability to learn faster and show better performance. In this project, the Statistical Physics of Learning framework is used to derive an exact mathematical description of the learning dynamics of the ReLU perceptron and ReLU Soft Committee Machines. The mathematical description consists of a system of ordinary differential equations that describe the evolution of so-called order parameters, which summarize the state of the network relative to the target rule. The correctness of the theoretical results is verified with simulations and several learning scenarios will be discussed.
2017

Segmentation of blood vessels in retinal fundus images
The inspection of the blood vessel tree in the fundus, which is the interior surface of the eye opposite to the lens, is important in the determination of various cardiovascular diseases. This can be done manually by ophthalmoscopy, which is an effective method of analysing the retina. However, it has been suggested that using fundus photographs is more reliable than ophthalmoscopy. Additionally, these images can be used for automatic identification of the blood vessels, which can be a difficult task due to obstacles such as low contrast with the background, narrow blood vessels and various blood vessel anomalies. A segmentation method with high accuracy can serve as a significant aid in diagnosing cardiovascular diseases, as it highlights the blood vessel tree in the fundus. In recent years, several segmentation methods have been proposed for the automatic segmentation of blood vessels, ranging from using cheap and fast trainable filters to complicated neural networks and even deep learning. In this paper we discuss and evaluate several of these methods by examining the advantages and disadvantages of each. Subsequently, we take a closer look at a filter-based method called B-COSFIRE. We study the performance of the method on test datasets of fundus images and we examine how the parameter values affect the performance. The performance is measured by comparing the extracted blood vessel tree with a manually segmented blood vessel tree. One of the datasets we consider is the recently published IOSTAR dataset and, if researchers have used the dataset already, we compare our results, using the IOSTAR dataset, with findings about blood vessel segmentation methods on this dataset in the field. Based on our findings there we discuss when B-COSFIRE is the preferred method to use and in which circumstances could it be beneficial to use a more (computationally) complex segmentation method. We also shortly discuss areas beyond blood vessel segmentation where these methods can be used to segment elongated structures, such as rivers in satellite images or nerves of a leave.